Resumo

Desenvolvendo o conceito de redes neuronais através da história do seu aparecimento, o autor pretende indiciar os seus contributos, designadamente para a compreensão do funcionamento do sistema nervoso nesta perspectiva que enquadra como sistémica. Para consubstanciar a exposição apoia-se no exemplo do reconhecimento de padrões, que deste modo reputa de paradigmático.

De igual modo, antecipa aplicações que desde logo enuncia ou prevê através do estado do conhecimento actual em tais domínios.

A associação ocasional entre computador e cérebro, seja encarando o computador como cérebro electrónico, seja o cérebro como computador natural, data dos primórdios da sua história. Nessas alturas logo surgem acalorados debates. O que de facto acontece é que, tal como os computadores têm dado importantes achegas para a compreensão do funcionamento cerebral, também o cérebro tem servido de modelo para uma abordagem biónica da informática; é a este último tipo de estruturas que se chama de redes neuronais.

Estas redes neuronais podem então definir-se como sistemas altamente dinâmicos de processamento paralelo da informação continuamente recebida; esta definição tem a vantagem de ir de encontro, exactamente, à tentativa de mimetizar o cérebro no que este tem de versatilidade e capacidade para intuir e inferir a partir de dados escassos porque incompletos ou confusos.

O que acontece quando aprendemos? Bom, o que de facto acontece é que, entre conceitos como compreender, memorizar, ou evocar, por um lado, e noções como neurónios, sinapses, impulso, e despolarização, por outro, vamos ter de observar, efectivamente, o que entra e o que surge, o que é fornecido e o que resulta, e ver depois então de que modo determinadas variáveis, seja o estado emocional ou outras, vão fazer variar os acontecimentos.

Quando nos voltamos para as redes neuronais, portanto, passamos a recorrer a todo um vocabulário novo, ou melhor, renovado. Não programamos uma rede neuronal, ensinamo-la. Não medimos a sua velocidade de processamento em instruções por segundo, mas em interconexões por segundo. De facto, as entradas e saídas são, aqui, em tudo idênticas às da computação convencional; o que pode ser tido como mais misterioso é o que vai acontecer entre umas e outras, entre as chamadas características definidoras, e pense-se por exemplo nos sinais e sintomas apresentados por um paciente, e as características classificadoras, tomadas agora como o diagnóstico sindromático capaz de enquadrar com determinada probabilidade o referido conjunto de sinais e sintomas.

A sua estrutura consiste num elevado número de elementos processadores, os neurónios formais, elementos esses que, enquanto neurónios simulados, admitem múltiplas entradas, os dendritos, mas uma só saída, o axónio; para além destes elementos processadores a rede neuronal é formada pelo seu esquema interconexional - topologia -, pelo modelo de aprendizagem, e pelo conhecimento do estado do sistema. É a este conjunto de aspectos que se chama de paradigma da rede, sendo que actualmente estão identificados cerca de 20.

Vejamos então de mais perto onde começam e terminam as analogias, tendo em mente o conceito de modelo tal como no-lo apresenta Ashby: "No electronic model of a cat´s brain can possibly be as true as that provided by the brain of another cat; yet what is the use of the latter as a model? Its very closeness means that it also presents all the technical features that make the first so difficult. From here on, then, I shall take as a basis the thesis that the first virtue of a model is to be useful." (Ashby, in Stogdill, 1970, p. 96)

Claude Shannon, sobretudo conhecido pela teoria matemática da comunicação (1949), terminou os seus estudos no MIT em 1938 com uma tese de doutoramento em que elaborou a demonstração da analogia de estrutura entre a álgebra de Boole e o funcionamento de circuitos eléctricos com comutadores; a concepção dos componentes dos computadores e a sua montagem, ainda hoje obedecem aos princípios fundamentais expostos por Shannon, pois que toda a informática assenta na descoberta de que os processos físicos podem ser exactamente isomorfos das operações lógicas. Um pouco mais tarde, em 1943, foram publicados dois artigos fundamentais. O primeiro, "Behaviour, Purpose and Teleology" (1), da autoria do matemático Norbert Wiener (1943), do fisiologista Arturo Rosenblueth e do engenheiro de electrónica Julian Bigelow, tomando como ponto de partida a analogia entre os seres vivos e as máquinas, propõe-se explicar o comportamento finalista dos animais através da causalidade circular que liga os organismos ao seu meio ambiente; é o famoso feedback. Do neuropsiquiatra Warren McCulloch (1943) e do matemático Walter Pitts (que contava então 18 anos), o segundo, "Logical Calculus of the Ideas Imminent in Nervous Activity", o qual identifica o sistema nervoso com uma máquina lógica e mostra que uma rede de neurónios formais, mediante órgãos de recepção, efecção e conexão, possui o mesmo poder de cálculo que uma máquina de Turing universal (1936). Estavam lançados os alicerces do empreendimento de epistemologia experimental que visa cercear cientificamente o espírito humano través do conceito de informação.

Reportando-nos aos elementos primários no que eles têm de comum, independentemente do tipo específico, vejamos então muito sucintamente em que aspectos os neurónios interligados em rede, uma vez que isoladamente de pouco servem, de que modo os neurónios, dizia, vão semelhar as portas lógicas e os circuitos de memória. Como resultado dos estímulos oriundos de inúmeros outros neurónios, ou do "mundo exterior" em se tratando de receptores, e uma vez alcançado um determinado limiar, vão-se dar, a nível neuronal, descargas eléctricas transmitidas ao longo do axónio, descargas essas conducentes, no botão terminal, a determinados fenómenos de membrana que culminam numa libertação quântica de mediador. O resultado, se transmitido ao exterior, será uma função de efecção, uma vez que é uma função linear do referido somatório; se transmitido a outros neurónios, vai depender da natureza do mediador, e isto porque pode resultar, por exemplo, em estabilização da membrana pós-sináptica. Id est, a ponderação da resposta neuronal está, de certo modo, dependente do somatório dos estímulos excitatórios e inibitórios recebidos a nível sináptico. E até aqui não temos dúvida em afirmar a possibilidade de emulação através de portas lógicas. A questão surge, de facto, no modo como os vários elementos se interligam, e de que resulta uma diferença capital, se bem que subtil na aparência: qualquer alteração nas conexões dos circuitos integrados de silício ou nas placas de circuitos impressos e eis que a finalidade que presidiu à sua concepção não mais será conseguida; na rede neuronal a que claudica um elo diminui certamente a performance, a eficácia, seja em termos de velocidade ou de fiabilidade, mas nada mais. Ou seja, muitas células morrem a todo o momento, mas a falha é colmatada e o declínio das capacidades gradual.

Em relação à arquitectura convencional, a que se tem chamado de "gargalo de Von Neumann" (vonNeumann 1948, publicado em 1951), pouco mais há a dizer além da referida incapacidade para lidar com o erro, a qual é, pois, inerente à sua concepção; na verdade, para obviar à desproporção entre a vasta quantidade de silício a que está acometida a "pouco movimentada" tarefa da memória e a minúscula mas "atarefada" unidade central de processamento, tudo o que tem sido feito, visando acelerar o processo, é minimizar até ao limite as distâncias e outros factores de resistência ao trânsito electrónico, e utilizar em paralelo múltiplos processadores controlados de modo a subdividir tarefas e evitar conflitos.

No processamento distribuído das redes neuronais, as actividades misturam-se e espalham-se por toda a rede, até porque toda e qualquer parte dessa mesma rede aparenta (e funciona como) qualquer outra. Assim, não é para admirar que, além da já referida capacidade para lidar com a falha, exista a capacidade igualmente distintiva para lidar com informação escassa, porque incompleta ou corrompida, seja a de uma imagem ténue ou a de um som com interferências. Finalmente, também diferenciadora é a característica notável de aprender com a experiência, a qual, se surge aqui naturalmente, já em termos de programação envolve problemas extremamente complexos. O facto de as redes neuronais não serem programáveis mas sim treináveis com exemplos, resulta de serem elas auto-organizáveis, id est, capazes de se estabelecer num estado significativo em termos do objectivo a alcançar, sem que seja necessária uma especificação algorítmica de como o alcançar. Por outras palavras pode dizer-se que, se por um lado não é possível saber qual o estado interno da rede através da observação do seu comportamento, por outro lado o seu conhecimento não é minimamente necessário. E por estes indícios podemos desde logo antecipar as linhas mestras da investigação nesta área, as quais vão desde a modelação do sistema nervoso para simulação e compreensão da ultaestrutura da cognição, até aos estudos sobre linguagem natural, ou de reconhecimento óptico de caracteres, ou seja, de reconhecimento de padrões (problema do caixeiro-viajante (2), análise de imagens médicas, etc.) e filtragem de ruído em geral.

E nesta altura a questão que se oferece é a de saber o que se passou desde os tempos de Pitts e McCulloch. E algo se passou de facto. Em 1948, no celebrado Cybernetics: or Control and Communications in the Animal and the Machine, Norbert Wiener (1948) propõe que o modus operandum do cérebro pode ser imanente da sua organização, pelo que sugere desde logo a construção de dispositivos que o tomem como modelo. Porém, se recordarmos as válvulas e os relais electromagnéticos então em uso, logo compreenderemos de que modo as exigências inerentes aos meios tecnológicos disponíveis não permitiram avançar significativamente nesta área; assim, o que restou de facto foram os avanços que este apport veio trazer para o domínio cognitivo.

Em 1952 o psicólogo inglês W. Ross Ashby (1952, 1966), no seu Design For a Brain propõe-nos o homeostato, um engenho analógico que concebe para, de algum modo, materializar o seu conceito de ultraestabilidade: tendência encontrada em sistemas naturais com base na sua capacidade para absorver ruído, id est, capacidade de manter um determinado nível de funcionamento apesar das variações do meio.

Por razões que não será difícil discorrer, no struggle for life das máquinas a informática seguiu o seu rumo na estirpe do computador; de facto, nada havia que pudesse justificar a orientação dos enormes custos da miniaturização para o serviço de uma eficácia duvidosa e em tudo semelhante à que desde logo existe no Homem levada ao seu expoente máximo, uma vez que se trata do seu modelo paradigmático. Assim é que o Perceptron, projectado por Frank Rosenblatt em 1955 (Rosenblatt, 1962), teve de esperar que a evolução dos computadores digitais viesse a permitir a simulação em software de redes com dimensões úteis, o que só viria a acontecer nos anos 60. Tratava-se de um sistema de visão artificial que simulava a retina por meio de células fotoeléctricas, órgão de entrada de uma rede neuronal simples que podia ser ensinada a reconhecer padrões visuais (Rosenblatt, 1958). O entusiasmo com que se discutia nessa altura a programação aleatória (Friedberg, 1958) e a abordagem de rede do tipo do Pandemonium (Selfridge, 1959), por exemplo, veio a esmorecer quando, por volta de 1969, os trabalhos de Marvin Minsky e Seymour Papert votaram o Perceptron ao ostracismo ao evidenciar a impossibilidade de expressão XOR, ou seja, de activar uma célula se uma e somente uma de duas células de entrada estiver activada. Vedando assim vastas áreas de processamento, consubstanciavam matematicamente o desinteresse nesta área. Até que às duas camadas de neurónios do Perceptron se juntou pelo menos mais uma, e aí o problema foi deslocado para a regra de aprendizagem capaz de se haver com camadas ocultas. Só mais recentemente é que este problema viria, em parte, a ser debelado, fazendo ressurgir a "fénix" conexionista; assim, e de um modo muito geral, o que se faz é comparar os valores de saída com os dos estímulos à entrada, reduzindo o erro através de uma função matemática que pondere e reajuste as ligações da rede, processo sucessivamente repetido até que seja alcançada uma distribuição estável.

O primeiro congresso internacional sobre redes neuronais do IEEE (3), em 1987, pode descrever-se em boa verdade como uma dúzia de apresentações perante uma assistência escassa. Enfim, além dos prelectores já havia quem tivesse ouvido falar no assunto a ponto de aparecer. Cerca de um ano depois, no segundo congresso internacional sobre redes neuronais, que decorreu em Julho de 1988 em San Diego, apareceram cerca de duas mil pessoas para ouvir falar em temas como "Neural Network Models and Their application to Handwritten Digit Recognition" ou "A Multilayer Perception Network for the Diagnosis of Low Back Pain". De então para cá começaram a ser comuns congressos de teor mais técnico como seja o de Pattern Recognition and Advanced Missile System. Fruto disso começaram também a aparecer firmas a comercializar tecnologia neuronal para resolver tarefas computacionais complexas. O Perceptron tem, finalmente, o seu herdeiro comercializado com o nome de WISARD, um projecto da Universidade de Brunel que consiste numa câmara de vídeo ligada a uma rede; treinado com expressões faciais, por exemplo, cedo ele se torna capaz de distinguir um sorriso de uma carranca. Também no domínio da voz humana a NETalk, construída na Universidade de Princeton, aceita texto como entrada, e acciona um sintetizador como órgão de saída; neste caso o ruído ininteligível das conexões aleatórias vem dar lugar à fala depois de um treino de ajuste das conexões por meio do fornecimento de palavras escritas a par com os respectivos fonemas. Outros casos ainda, capazes de ilustrar os avanços notáveis alcançados por esta via são o do reconhecimento da fala, aprendizagem de que se encarrega a TDNN (4) (Waibel, 1989), e o projecto em curso na Carnegie Mellon de um veículo de navegação autónoma, o NAVLAB, desde logo pilotado com precisão pelo ALVINN (5) (Pomerleau, 1989) a uma velocidade de cerca de 3 milhas e meia, em diferentes condições climatéricas e de luz.

Actualmente há dois congressos por ano, designadamente o IJCNN (6) do Verão e o do Inverno, ambos patrocinados pela INNS (7) e pelo IEEE, tendo decorrido o último em 19 de Junho de 1989, e seguindo-se o do Inverno, a decorrer a 15 de Janeiro próximo (8).

Face a problemas que requeiram decisões por aproximação, e não por correspondência exacta, a questão que o programador esclarecido sobre esta matéria se põe de hoje em dia já não é sobre se a rede neuronal tem ou não aplicação, mas antes sobre qual o paradigma a aplicar numa determinada situação.

Ao descrever o modo como os neurónios semelham as portas lógicas designamos, no fundo, as cinco funções passíveis de caracterizar a actividade dos neurónios formais. São elas:

Entrada, uma vez que qualquer neurónio deve poder ser estimulado por outros, usando tais valores para calcular o seu próprio nível de actividade: os binários 1 e 0 para activo e inactivo respectivamente, na proposta de McCulloch-Pitts; de facto podem ser de 1 e -1, ou até de valores discretos, seja entre 0 e 1.

Ponderabilidade, na medida em que deve poder reagir mais ou menos a uma dada entrada, seja ela excitatória ou inibitória. Tal peso irá pois, ser multiplicado pela entrada recebida, determinando assim o valor efectivamente utilizado enquanto função linear do estímulo.

Somatório, posto que o estímulo resulta de todas as entradas positivas e negativas uma vez ponderadas.

Limiar a partir do qual o somatório irá determinar a efecção, limiar esse que permite discriminar valores de entrada diferentes, bem como eliminar o ruído branco.

Função de retrotransmissão que permita, além do que acontece na célula de McCulloch-Pitts, em que a saída é determinada conforme a entrada alcança (1) ou não (0) o limiar, que permita, dizia, caso o limiar seja alcançado, relacionar a saída com a entrada de modo tão complexo quanto se pretenda. Este é aliás, um dos meios que confere utilidade extrema às redes neuronais, seja por exemplo em matéria de filtrar ruído.

Além disso as redes neuronais tendem a arranjar-se em camadas, recebendo as células de uma camada as suas entradas, em regra, dos neurónios da camada precedente. A ideia é obter um esquema de ligações, e uma distribuição de pesos, por forma a conseguir que determinadas saídas se relacionem de forma considerada útil com os valores das entradas. Isto consegue-se, não mais recorrendo a uma sequência algorítmica de instruções, mas através de um treino por meio de exemplos, treino esse capaz de permitir o desenvolvimento iterativo de uma combinação de pesos que faculte a saída pretendida. Um dos principais alvos de estudo nesta área é precisamente o das regras para alteração dos pesos, visando encerrar em fórmulas as leis da aprendizagem, por forma a acelerar o processo e alcançar rapidamente uma situação estável. Mas talvez não seja este o local mais adequado para nos debruçarmos sobre a análise detalhada dos paradigmas de aprendizagem. Para facilitar a compreensão, no entanto, julgo que talvez seja mais conveniente, isso sim, que nos detenhamos sobre a questão das topologias. E isto porque, para enfrentar uma determinada tarefa, muitas topologias há, e se a correcta nos pode dar uma solução extremamente simples, já uma escolha errada pode resultar numa complicação desnecessária ou até numa ausência de solução.

Vejamos então, como exemplo ilustrativo, em que consiste o reconhecimento de padrões e de que modo pode ser alcançado. No fundo, consiste em memorizar um padrão e reconhecê-lo depois, tolerando as ambiguidades. O que se constata, porém, é que há mais do que um paradigma para o conseguir, cada um deles com a sua especificidade. Um deles é o da associação de padrões. Um outro é o da classificação. O primeiro consiste em manipular pares de padrões por forma a fornecer um deles como saída, quando recebe o outro como entrada; esta configuração, em que a rede associa o padrão de saída com o de entrada, é-lhe ensinada, ou então fornecida explicitamente através das já mencionadas fórmulas com as regras da ponderabilidade. O paradigma da classificação, análogo enquanto associador das entradas com as saídas, difere na medida em que categoriza os padrões de entrada de acordo com determinadas formas de os agrupar; ora isto vai permitir à rede fornecer uma saída correcta quando confrontada com uma entrada distorcida ou incompleta.

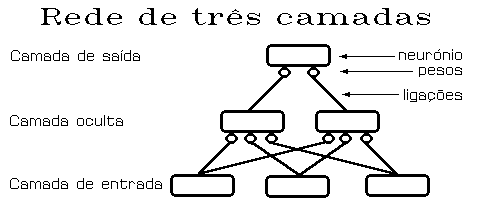
Vamos então definir uma topologia por forma a podermos começar a aproximar-nos da ilustração pretendida. A nossa rede (figura 1), com três camadas, utilizará uma delas para entrada, outra como oculta, e a terceira para saída. Em cada uma das camadas os respectivos neurónios estão todos ligados aos da seguinte, e o seu limiar de activação está sempre dependente de uma mesma função. Finalmente, a função de propagação é sempre um somatório ponderado, activando-se as ligações na direcção da camada de saída - rede de antero-alimentação.

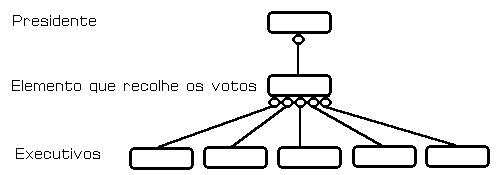
Nas redes mais simples a função de activação é linear, não modificando a entrada, pelo que a função de propagação transmite o seu resultado directamente para a saída. Suponhamos uma reunião da direcção numa empresa em que os accionistas se fazem representar por 5 executivos (figura 2). Há um elemento que recolhe os votos e que transmite o resultado da votação ao presidente em função do voto a favor ou contra de cada um dos votantes e do número de accionistas por ele representado. Nesta rede o peso entre a camada de entrada e a oculta reside no número de accionistas representado por cada votante; entre a oculta e a de saída o peso é 1.0 uma vez que o presidente parte do princípio que o membro que recolhe os votos é honesto.

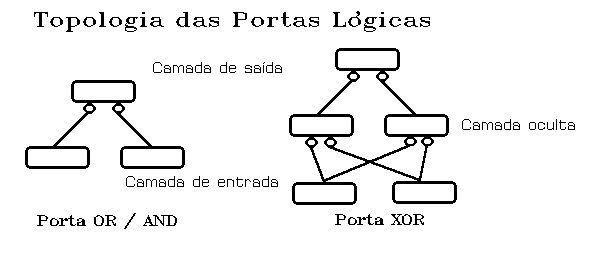
Complicando um pouco mais a nossa rede, vamos imaginar que a resposta assume determinado valor se a entrada ultrapassar um limiar determinado por uma função linear, e um outro de contrário. É exactamente isto o que acontece nas portas lógicas, em que o limiar é determinado por uma função binária: existência ou não de resposta. Para uma porta de duas entradas, como a OR ou a AND (porção esquerda da figura 3), pode usar-se uma camada de entrada de dois neurónios e uma camada de saída de um neurónio; já a XOR (porção direita da figura 3), vai requerer uma camada oculta de dois neurónios, por forma a poder executar a operação de exclusão, posto que tem de comparar as duas entradas da perspectiva de cada uma delas.

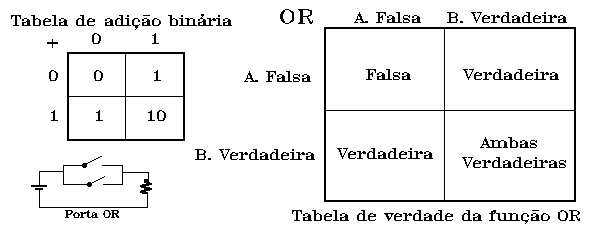
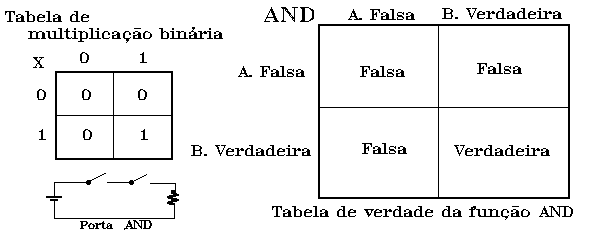
Com efeito, podemos estabelecer, a partir das respectivas tabelas de verdade (figura 4 e 5), que o neurónio de saída da porta OR é estimulado por uma sinapse oriunda de cada um dos neurónios de entrada, podendo ser activado por qualquer delas. O mesmo se passa na porta AND, porém aqui o limiar tem de ser duplicado e reduzido a zero após qualquer estimulação; não fora esta acção inibitória e uma dupla estimulação de um dos neurónios de entrada poderia determinar uma resposta. Quanto à porta XOR, provavelmente um mecanismo idêntico ao utilizado por sistemas biológicos para comparação de padrões, ela disporá de um neurónio de saída que traduz uma porta OR em relação aos dois intermédios; cada um destes, por seu turno, estará ligado por uma sinapse excitatória a um dos de entrada, e por uma inibitória ao outro. Deste modo, para que um dos neurónios intermédios atinja o limiar, o outro não pode estar a ser estimulado.

Vejamos então de que modo se pode alcançar o reconhecimento óptico de caracteres (OCR), isto é, de que modo pode um determinado padrão óptico ser traduzido num código que o represente, seja por exemplo o do ASCII (American Standard Code for Information Interchange); e até aqui, desde que o padrão introduzido corresponda exactamente ao que à partida se associou ao respectivo código, nada de novo. Onde as redes neuronais se tornam particularmente adequadas, conforme foi dito, é a reconhecer padrões que não constituem tais decalques dos que se lhes ensinou, antes fornecendo uma resposta com o respectivo grau de certeza.

Antes de avançar, no entanto, importa precisar o conceito de nódulo. Este refere-se a um conjunto de neurónios pertencentes a uma mesma camada, mas por tal forma interrelacionados que competem mutuamente para serem os representantes exclusivos do grupo; por outras palavras: o neurónio mais perto do limiar é levado a alcançá-lo, ao passo que todos os outros são inibidos; no caso de haver neurónios equidistantes, é "despolarizado" o primeiro a ser encontrado, sem que com isso diminua a precisão, uma vez que aos mesmos valores corresponderão graus de certeza idênticos.

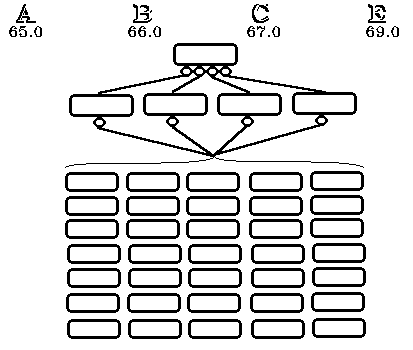
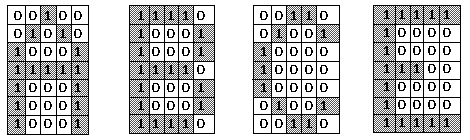
Ao conjunto formado pela camada de entrada com a oculta costuma chamar-se de Perceptron (Rosenblatt, 1958). É uma rede cujos neurónios podem assumir um de dois estados, conforme o limiar é ou não alcançado; além disso, o somatório de todas as entradas de um neurónio da camada oculta, uma vez ponderadas, será sempre igual ou inferior a 1.0. A camada oculta com a camada de saída, por seu turno, formam uma rede linear. Quanto aos nódulos, eles só existem na camada oculta, formando esta, no caso de que nos temos vindo a aproximar, um único nódulo (figura 6). Deste modo torna-se possível classificar tantos padrões de entrada quantos os neurónios da camada oculta, atribuindo-se, por exemplo, cada um deles a uma das letras do alfabeto. A partir daqui, vai ser preciso ensinar à rede quais os padrões que produzem este ou aquele resultados, a menos que se saiba o que a rede aprende, construindo atalhos que permitam acelerar o processo. É o que faremos se, por exemplo, nos limitarmos ao reconhecimento de um só caracter.

Cada uma das letras é então lida e apresentada à rede, seleccionando-se o neurónio da camada oculta ainda não atribuído, o qual passará então a ponderar cada uma das entradas oriundas da primeira camada, naturalmente. O peso de cada sinapse por cujo axónio atravessa um impulso será igual a 1.0 a dividir pelo número total de neurónios estimulados; já o peso de cada sinapse não activada vai ser de 0.0. Quanto ao peso das sinapses entre os neurónios da camada oculta e os da de saída, ele vai ser igual ao do valor numérico do código que assim pretendemos associar ao padrão de entrada. Aprendidos determinados caracteres, sempre que se lhe apresente um novo padrão a rede dir-nos-á qual dos padrões aprendidos mais se lhe assemelha.

Mas não devemos concluir de toda esta simplicidade aparente, ou pelo facto de esta tecnologia de processamento da informação tomar como modelo o sistema nervoso, que ela é por isso mesmo menos bem fundamentada. Com efeito, certos tipos de rede têm profundas bases matemáticas. Sem querer penetrar em tais fundamentos, até porque, tendo feito do sistema nervoso a minha principal área de interesse, não me julgo como a pessoa mais indicada para o fazer, não quero no entanto deixar de referir as implicações em termos de aprendizagem da técnica de retrotransmissão. Esta, cuja eficácia já foi mencionada como particularmente importante em termos de filtro de ruído de fundo que se supõe aleatório, esta, dizia, baseia-se numa configuração da rede capaz de estabelecer uma relação entre as variáveis de entrada e as de saída, por forma a minimizar o erro entre a saída fornecida pela rede e a saída que se pretende correcta. Após minimizar o erro, ou seja, depois de ensinar a rede, podemos dizer que ela aprendeu a relação entrada / saída, podendo agora dar respostas próximas das correctas apesar dos dados fornecidos serem incompletos. Temos pois, em resumo, uma rede constituída por três camadas, o que em regra é suficiente, rede essa cujas respostas se relacionam com os dados fornecidos através de uma função não linear. As modificações no peso das sinapses tem de ser feita, por um lado, entre a segunda e a terceira camadas, mas também tem, por outro, de ser transmitida para trás até às que ligam a primeira à segunda. E assim se determina o erro, o qual vai diminuindo à medida que se modifica, proporcionalmente, o peso. Ora a constante de proporcionalidade é o que se designa por taxa de aprendizagem; digamos, exemplificando, que se essa taxa for de 0.5, isso significa que a variação do peso é função de metade do erro. Daqui poder-se-ia concluir que aumentar a taxa de aprendizagem seria um factor positivo de aprendizagem, dado que esta se torna mais rápida. Acontece porém que isso pode conduzir a oscilações mais amplas, e impedir mesmo a estabilização, ou então levar a rede a convergir para uma solução inadequada. Para obviar a isso vai-se entrar em linha de conta com o momento, isto é, vai-se fazer depender a variação no peso da anterior, o que resulta numa progressão mais suave. Ou seja:

Cada nova alteração do peso =

(taxa de aprendizagem) * (função do erro) + (momento) * (alteração anterior)

---

(1) Comportamento, finalidade e teleologia
(2) Caixeiro-viajante que deve achar o caminho mais curto para percorrer de modo a passar num determinado número de cidades; tendo em mente, por exemplo, que para 10 cidades existem 1 814 400 de alternativas (10!/2), logo se compreende a inexequibilidade da via algorítmica que consiste em calcular e comparar exaustivamente as alternativas.
(3) Institute of Electrical and Electronics Engineers
(4) Time-Delay Neural Network
(5) Autonomous Land Vehicle In a Neural Network
(6) International Joint Conference on Neural Network
(7) International Neural Network Society. Para obter informações sobre como tornar-se membro deve dirigir-se a Frank Polkinghorn na seguinte direcção: INNS Membership, P.O. Box 441166, Fort Washington, Md. 20744, U.S.A. [Telefone: (301) 839-2114].
(8) No Omni Shoreham Hotel, em Washington, DC

Agradecimentos

O autor quer deste modo expressar a sua gratidão aos organizadores das II JORNADAS DE INFORMÁTICA E IMAGEM MÉDICAS DO PORTO na pessoa do Dr. F. Reis Lima pelo amável convite que lhe foi dirigido no sentido de fazer a exposição a que se refere o presente texto.

Bibliografia

1. Almeida Luis B. Backpropagation in Perceptrons with Feedback. In Rolf Eckmiller and Christoph Malsburg (eds) Neural Computers. Berlin: Springer-Verlag, 1989.
2. Arbib Michael A. Brain, Machines, and Mathematics. Berlin: Springer-Verlag, 1987.
3. Ashby W Ross. Design for a Brain (Col. Science Paperbacks). London: Chapman & Hall, 1952, 1966.
4. Cannon WB. The Wisdom of the Body. Norton, 1939.
5. Eckmiller Rolf & Malsburg Christoph (eds). Neural Computers: Proceedings of the NATO Advanced Research Workshop on Neural Computers. Berlin: Springer-Verlag, 1988.
6. Friedberg RM. A Learning Machine: Part I IBM Journal 1958 (Jan.): 2-13.
7. King Todd. Using Neural Networks for Pattern Recognition. Dr. Dobb's Journal 1989 (Jan.): 14-28.
8. Klimasauskas Casey. Neural Nets and Noise Filtering. Dr. Dobbs Journal 1989 (Jan.): 32-48.
9. Kohonen Teuvo. Self-Organization and Associative Memory. Berlin: Springer-Verlag, 1988.
10. McClelland JL and Rumelhart DE. Explorations in Parallel Distributed Processing: A Handbook of Models, Programs and Exercises. Cambridge, MA: MIT Press, 1988.
11. McCulloch WS and Pitts WH. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943; 5: 115-133.
12. Minsky ML and Papert S. Perceptrons: An Essay in Computational Geometry. Cambridge, MA: MIT Press, 1969, 1988.
13. Obermeier Klaus K. and Barron Janet J. Time to Get Fired Up. BYTE 1989 (Aug.): 214-224.
14. Pomerleau DA. ALVINN: An Autonomous Land Vehicle in a Neural Network. In D. S. Touretzky (ed) Advances in Neural Information Processing Systems 1. San Mateo, CA: Morgan Kaufmann Publishers, 1989.
15. Rosenblatt F. The Perceptron, a Probabilistic Model for Information Organization and Storage in the Brain. Psychological Review 1958; V65: 363-408.
16. Rosenblatt F. Principles of Neurodynamics. Spartan Books, 1962.
17. Rosenbleuth A, Wiener N and Biglow J. Behaviour, purpose and teleology. Philos. Sci. 1943; 10: 18-24.
18. Rumelhart David E, McClelland James L (eds) and the PDP Research Group. Parallel Distributed Processing. Cambridge, MA: MIT Press, 1986, 1987.
19. Selfridge OG. Pandemonium: a Paradigm for Learning In D Blake & A Uttley (eds.) Proc. Symposium on Mechanization of Thought Processes. London: H. M. Stationery Office, 1959: 511-531.
20. Shannon Claude E. A symbolic Analysis of Relay and Switching Circuits. Trans. Amer. 1938; IEE, 57.
21. Shannon Claude E and Weaver W. The Mathematical Theory of Communication. Urbana, Chicago, London: University of Illinois Press, 1949.
22. Stogdill RN (ed). The Process of Model Building. Ohio State University Press, 1970.
23. Touretzky David S and Pomerleau Dean A. What's Hidden in the Hidden Layers? BYTE 1989: 227-233.
24. Turing Allan. On Computable Numbers with an Application to the Entscheidungs Problem. Proceeding of the London Mathematical Society, 2ª Serie. 1936 (12 Nov); V42 (3ª parte): 230-265.
25. Turing Allan. On Computable Numbers with an Application to the Entscheidungs Problem. Proceeding of the London Mathematical Society, 2ª Serie, 1937 (20 Maio); V43 (7ª parte): 546-550.
26. Verissimo R. Introdução às Aplicações da Microinformática na Investigação; Inteligência Artificial. Texto de apoio à palestra proferida no Instituto de Histologia e Embriologia de Abel Salazar (Março 25). Porto, Faculdade de Medicina, 1987.
27. vonNeumann John. The general and logical theory of automata In LA Jeffer (ed) Cerebral Mechanisms in Behaviour: The Hixon Symposium. Wiley, 1951: 1-32.
28. Waibel Alex and Hampshire John. Building Blocks for Speech. BYTE 1989; 235-242.
29. Weber Jack. Uma janela para o cérebro. PCW (ed. port.), 1989; (Fev.): 70-75.
30. Wiener Norbert. Cybernetics Mass.: MIT Press, 1948.